A force doublet is commonly defined as two equal but opposite forces acting in an infinite medium
Question:
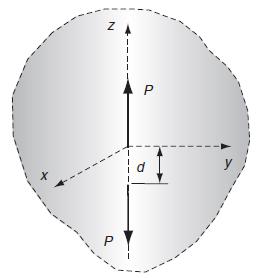
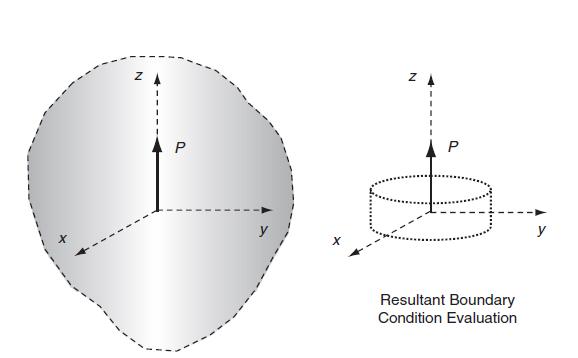
A force doublet is commonly defined as two equal but opposite forces acting in an infinite medium as shown in the following figure. Develop the stress field for this problem by superimposing the solution from Example 13.1 onto that of another single force of –P acting at the point z =–d. In particular, consider the case as d→0 such that the product Pd→D, where D is a constant. This summation and limiting process yield a solution that is simply the derivative of the original Kelvin state. For example, the superposition of the radial stress component gives:
![lim [o,(r,z) o,(r,z+ d)] : = OR dor z TRO -d- D 8T (1- - v) dz The other stress components follow in an](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/1/3/6/03065a24f9e562a81705136029745.jpg)
Data from example 13.1



Equation 13.5.9
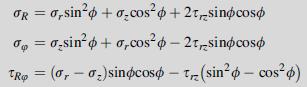
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.
Question Posted:





