Consider the two-dimensional case described in Exercise 3.22 with no body forces. Show that equilibrium equations are identically satisfied if the stresses are expressed in the form:

where ∅(x, y) is an arbitrary stress function. This stress representation will be used in Chapter 7 to establish a very useful solution scheme for two-dimensional problems.

Data from exercise 3.22

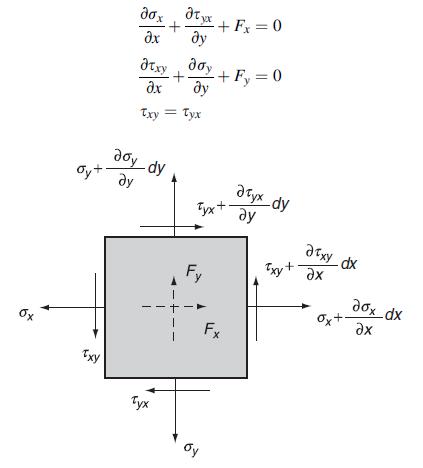
Consider the equilibrium of a two-dimensional differential element in Cartesian coordinates, as shown in the following figure. Explicitly sum the forces and moments and develop the two-dimensional equilibrium equations:

Transcribed Image Text:

Ox 22 12: 22 07 Tr 22