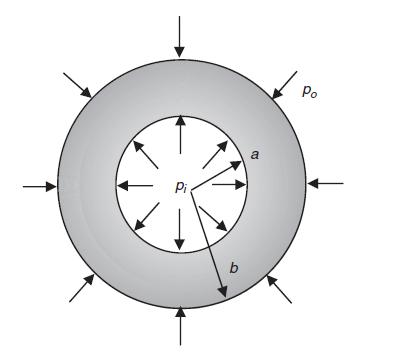
For the hollow cylinder problem illustrated in Fig 14 5, show that the usual restrictions on Poissons ratio, 0 v 1 2, and n 0 imply that Using these results, develop arguments to justify that the stresses in solution (14 2 7) must satisfy r 0 in the cylinders domain Thus, stresses in the nonhomogen...

With k 44nv kn 41nv For the case with 0 v12 n 0n 4 k n 42n 42nz ...

For the hollow cylinder problem illustrated in Fig. 14.5, show that the usual restrictions on Poissons ratio,

Question:

For the hollow cylinder problem illustrated in Fig. 14.5, show that the usual restrictions on Poisson’s ratio, 0 ≤ v≤ 1/2, and n > 0 imply that:

-2+k+n0, -2-k+n0 2 + kv - nv k-n+2v > 1, 2-kv-nv k+n-2v <1

Using these results, develop arguments to justify that the stresses in solution (14.2.7) must satisfy σ_rθ > 0 in the cylinder’s domain. Thus, stresses in the nonhomogeneous problem have behavior similar to those of the ungraded case.

Fig 14.5

Equation 14.2.7

or = e Pia(2+k-n)/2 bk - ak [ r(-2+k+n)/2 _ Bp(-2-k+n)/2] Pia(2+k-n)/2 [2 + kv- k - nv k-n+2v 2-kv - nv

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Elasticity Theory Applications And Numerics

ISBN: 9780128159873

4th Edition

Authors: Martin H. Sadd Ph.D.

See More Books

Question Posted: Jan 15, 2024 05:02 AM

See More Questions

For the hollow cylinder problem illustrated in Fig. 14.5, show that the usual restrictions on Poissons ratio,

Question:

-2+k+n0, -2-k+n0 2+kv - nv k-n+2v > 1, 2-kv-nv k+n-2v <1

Step by Step Answer:

With k 44nv kn 41nv For the case with 0 v12 n 0n 4 k n 42n 42nz...View the full answer

Elasticity Theory Applications And Numerics

Students also viewed these Engineering questions