It was discussed in Section 3.4 that for the case of ranked principal stresses ( 1 >

It was discussed in Section 3.4 that for the case of ranked principal stresses (σ₁ > σ₂ > σ₃), the maximum shear stress was given by S_max = (σ₁– σ₃)/2, which was the radius of the largest Mohr circle shown in Fig. 3.7. For this case, show that the normal stress acting on the plane of maximum shear is given by N = (σ₁ + σ₃)/2. Finally, using relations (3.4.9) show that the components of the unit normal vector to this plane are n_i =± (1, 0, 1)/√2 . This result implies that the maximum shear stress acts on a plane that bisects the angle between the directions of the largest and the smallest principal stress.

Fig 3.7

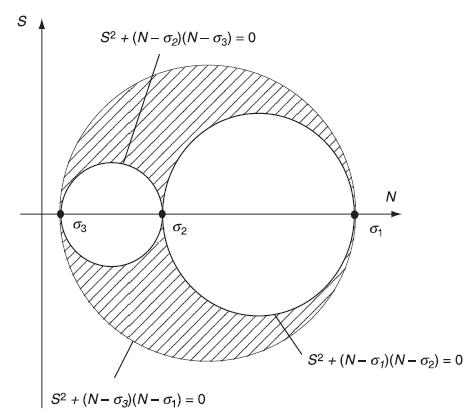
Equation 3.4.9

Transcribed Image Text:

S 03 S2+ (N-0)(N-03) = 0 02 S2 + (N-03)(N-0) = 0 01 N S2+(N-0)(N-0) = 0