Explicitly show that the stress state given in Example 3.1 will reduce to the proper diagonal form

Question:

Explicitly show that the stress state given in Example 3.1 will reduce to the proper diagonal form under transformation to principal axes.

Data from example 3.1

For the following state of stress, determine the principal stresses and directions and find the traction vector on a plane with unit normal n = (0, 1, 1)/ √2:

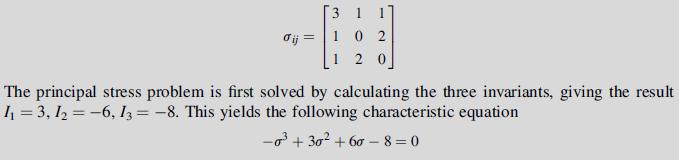
dij 1 0 2 120 The principal stress problem is first solved by calculating the three invariants, giving the

The roots of this equation are found to be σ = 4, 1, –2. Back substituting the first root into the fundamental system [see (1.6.1)] gives:

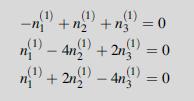
(1) (1) (1) -n +1 +n3 = 0 - 4ng+2n n() - Any) n + 2n +2ng) - 4ng (1) (1) = 0 = 0

Equation 1.6.1

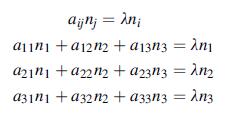
ain; = ani dinj ayn + 12m2 + a13n3 = a2in1 + a22m + a23n3 = n a3in1 + 432m2 + 3303 = in3

Solving this system, the normalized principal direction is found to be n ⁽¹⁾ = (2, 1, 1)/ √6. In similar fashion the other two principal directions are n ⁽²⁾ = (–1, 1, 1)/ √3, n ⁽³⁾ = (0, –1, 1)/ √2. The traction vector on the specified plane is calculated by using the relation: