A windmill has an approach velocity \(V_{1}=24 \mathrm{mph}(35.3 \mathrm{ft} / \mathrm{s})\) and a blade diameter of \(100 \mathrm{ft}\). The blade rotates at \(15 \mathrm{rpm}\). Figure P12.51 shows a blade cross-sectional profile and the velocity diagrams for a short section of the blade at a radius of \(r=25.0 \mathrm{ft}\). The outlet relative velocity \(W_{2}\) is tangent to the blade at the outlet so \(\beta_{2}=\beta_{2}^{\prime}=30^{\circ}\). The air density is constant as it flows over the blade. Assume that the flow area for the mass flow rate that interacts with this short section of the blade is the same upstream and downstream of the blade (i.e., \(A_{1}=A_{2}\) ). Find the velocity diagram downstream of the blade by finding \(U, W_{2}, V_{2}\), and \(\alpha_{2}\).

Figure P12.51

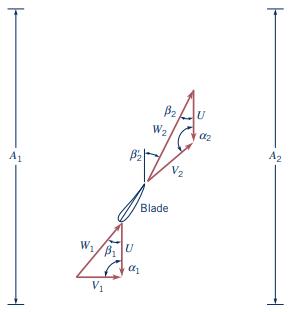
A1 B W BU V B U W2 02 A2 Blade