The house shown is flooded by a broken waterline. The owners siphon water out of the basement
Question:
The house shown is flooded by a broken waterline. The owners siphon water out of the basement window and down the hill, with one hose, of length L, and thus an elevation difference of h to drive the siphon. Water drains from the siphon, but too slowly for the desperate home owners. They reason that with a larger head difference, they can generate more flow. So they get another hose, same length as the first, and connect the 2 hoses for total length 2L. The backyard has a constant slope, so that a hose length of 2L correlates to a head difference of 2h.
a. Assume no head loss, and calculate whether the flow rate doubles when the hose length is doubled from Case 1 (length L and height h) to Case 2 (length 2L and height 2h).
b. Assume hL = 0.025(L/D)(V2/2g), and calculate the flow rate for Cases 1 and 2, where D = 1 in., L = 50 ft ., and h = 20 ft . How much of an improvement in flow rate is accomplished in Case 2 as compared to Case 1?
c. Both the husband and wife of this couple took fluid mechanics in college. They review with new appreciation the energy equation and the form of the head loss term and realize that they should use a larger diameter hose. Calculate the flow rate for Case 3, where L = 50 ft , h = 20 ft , and D = 2 in. Use the same expression for hL as in part (b). How much of an improvement in flow rate is accomplished in Case 3 as compared to Case 1 in part (b)? 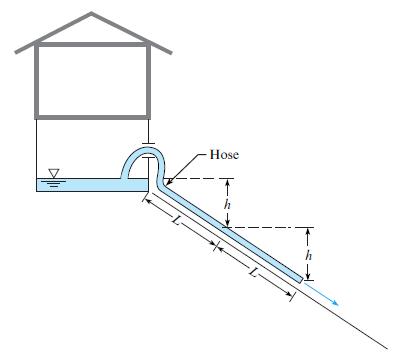
Step by Step Answer:

Engineering Fluid Mechanics
ISBN: 9781118880685
11th Edition
Authors: Donald F. Elger, Barbara A. LeBret, Clayton T. Crowe, John A. Robertson





