If a body contains no planes of symmetry, the principal moments of inertia can be determined mathematically.
Question:
If a body contains no planes of symmetry, the principal moments of inertia can be determined mathematically. To show how this is done, consider the rigid body which is spinning with an angular velocity ω, directed along one of its principal axes of inertia. If the principal moment of inertia about this axis is I, the angular momentum can be expressed as H = Iω = Iωx i + Iωyj + Iωzk. The components of H may also be expressed by Eqs. 21–10, where the inertia tensor is assumed to be known. Equate the i, j, and k components of both expressions for H and consider ωx, ωy, and ωz to be unknown. The solution of these three equations is obtained provided the determinant of the coefficients is zero. Show that this determinant, when expanded, yields the cubic equation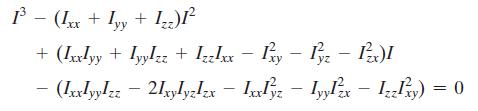
The three positive roots of I, obtained from the solution of this equation, represent the principal moments of inertia Ix, Iy, and Iz.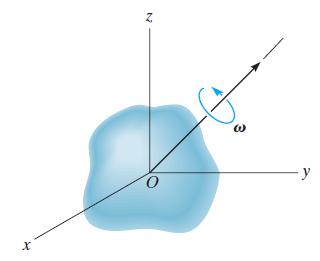
Step by Step Answer:

Engineering Mechanics Statics & Dynamics
ISBN: 9780134895154
15th Edition
Authors: Russell C. Hibbeler





