A very simple version of the normative model described in the text involves a simple economic growth

Question:

A very simple version of the normative model described in the text involves a simple economic growth process converging to a steady-state, where values do not change over time. ${ }^{14}$

A simple model of the climate would involve a greenhouse gas accumulation equation and a temperature change equation: $d M / d t=\beta E(t)-\delta M(t)$ and $d T / d t=\alpha[\lambda M(t)-$ $T(t)]$ where $M$ is the stock of greenhouse gases (in billions of tons), $E(t)$ is the emission level (in billions of tons per year) and $T(t)$ is the global temperature increase (in ${ }^{\circ} \mathrm{C}$ over preindustrial levels), with values of $\beta, \delta, a$, and $\lambda$ of $0.50,0.005,0.02$, and 0.003 , respectively. Note that in 2005 world GDP was about $\$ 60$ trillion and approximately 8 billion tons of carbon were emitted (in the form of carbon dioxide equivalent).

a. Using the simple climate model, what is the relationship between the steady-state emission level $\left(E^{*}\right)$ and the steady-state temperature $\left(T^{*}\right)$ ? Recall that steady-state means that neither $M$ nor $T$ are changing.

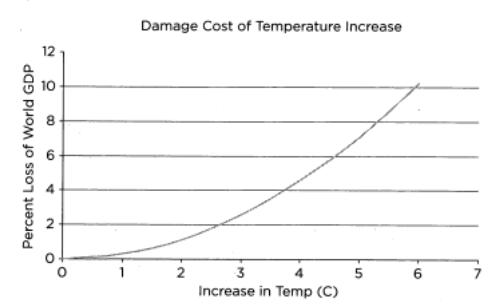
b. Convert Figure 2.2 into a plot of the damage as a function of temperature change, assuming steady-state global GDP of US $\$ 100$ trillion per year. Generate a plot of the marginal damage (\$ per degree temperature increase) as a function of the temperature rise.

c. Use the results from parts (a) and (b) to generate a plot showing the marginal damage ( $\$$ per ton of carbon emissions) as a function of the fraction of emissions controlled (assume steady-state uncontrolled emissions of 12 billions tons of carbon).

d. What level of emission control balances the marginal cost of control with the marginal damage?

Figure 2.2

image text in transcribed