A researcher used data on these three variables for 60 universities randomly selected from the 229 national universities in U.S. News & World Report’s rankings of U.S. colleges and universities: Y = graduation rate (mean 59.65), X₁ = student body’s median math plus reading SAT score (mean 1,030.5), and X₂ = percent of student body with GPAs among the top 10 percent at their high school (mean = 46.6). He found a statistically significant positive relationship between SAT scores and graduation rate: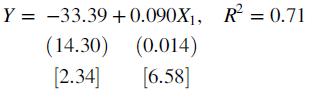

The standard errors are in parentheses and the t values are in brackets. He also found a statistically significant positive relationship between GPA and graduation rate: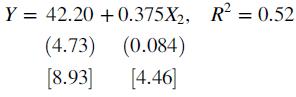

But when he included both SAT scores and GPAs in a multiple regression model, the estimated effect of GPAs on graduation rates was very small and not statistically significant at the 5 percent level: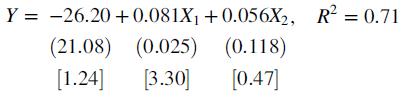

a. He suspected that there was an error in his multiple regression results. Is it possible for a variable to be statistically significant in a simple regression but not significant in a multiple regression?

b. Do you think that X₁ and X₂ are positively correlated, negatively correlated, or uncorrelated?

c. If your reasoning in b is correct, how would this explain the fact that the coefficients of X₁ and X₂ are lower in the multiple regression than in the simple regression equations?

Transcribed Image Text:

Y = -33.39+0.090X1, R2 = 0.71 == (14.30) (0.014) [2.34] [6.58]