An APT model is based on two independent systematic factors (F_{1}) and (F_{2}), both with zero expected

Question:

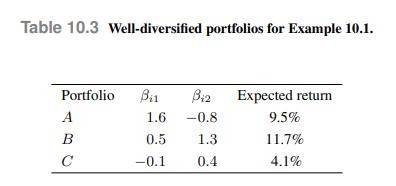
An APT model is based on two independent systematic factors $F_{1}$ and $F_{2}$, both with zero expected value (centered model). We assume that the holding period is one year, and the annual risk-free rate is $4 \%$. We are given the three well-diversified portfolios displayed in Table 10.3. Let us find the coefficients of an APT model based on portfolios $A$ and $B$, and check whether the introduction of portfolio $C$ creates an arbitrage opportunity.

To find the first answer, we solve the system of linear equations

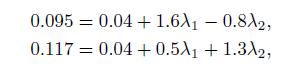
image text in transcribed

which yield =0.0537, and=0.0386. Note that the problem data give =0.04 directly.

Hence, according to APT, the equilibrium expected return of portfolio $C$ should be

which is larger than the expected return in Table 10.3. If we believe the parameter estimate in the table, then we have an arbitrage opportunity. Using portfolios $A$ and $B$, as well as the risk-free asset, we may generate a portfolio (let us call it portfolio $D$ ) with the same risk exposure of portfolio $C$, but a larger expected return. Hence, we should short portfolio $C$ and buy portfolio $D$. To find a combination of $A$ and $B$ with the same risk exposure as $C$, we solve the following system:

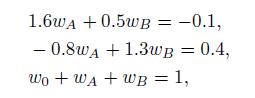
image text in transcribed

where $w_{0}$ is the weight of the risk-free asset (which has zero beta by definition). Note that we need the third equation to obtain a set of normalized weights, which would not be obtained by using only the first two equations. Solving this system, we find $w_{A}=0.1331 w_{B}=$ $0.2258 w_{0}=0.9073$.
Given these weights, the return of the resulting portfolio $D$ is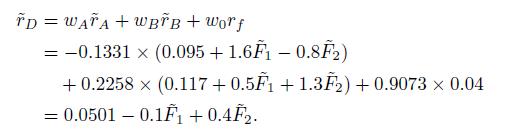
image text in transcribed

The expected return of portfolio $D$ is, in fact, 0.0501, as predicted by the consistency condition in Eq. (10.21). Finally, we build a long short portfolio with $w_{C}=1$ (short portfolio $C$ ) and $w_{D}=1$ (buy portfolio $D$, which replicates the risk exposure of $C$ ). The portfolio is both dollar-neutral and beta-neutral. Assuming no specific risk (and no estimation errors in our models), its return is deterministic: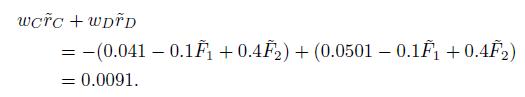
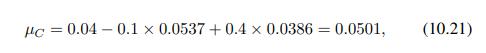
image text in transcribed