Here we consider a seemingly trivial problem: How to hedge a single systematic risk factor away, when there is no specific risk. Let us consider two well-diversified portfolios whose returns follow the single-factor model 

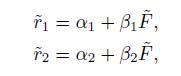
where we have streamlined notation a bit to account for the presence of one risk factor. Without loss of generality, let us assume a centered model with =0, so that each alpha is the expected portfolio return. It is easy to find a portfolio with suitable weights, such that the common risk factor is hedged away. From

we see that the portfolio exposure to the risk factor is given by the term within brackets. By setting

we find a weight

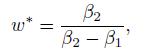
such that the portfolio is beta-neutral. However, since the resulting portfolio is risk-free, no-arbitrage implies that it must earn the risk free return, no more, no less. The return of the portfolio with weights and is

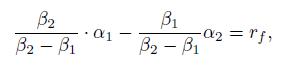
which may be rewritten as

We have not made any assumption about the two portfolios we are considering. Hence, this equality must hold for any pair of well diversified portfolios, and the ratios in Eq. 10.22 must be a constant depending only on the risk factor:

Thus, the expected return is just the risk-free rate plus the risk exposure multiplied by a coefficient which may be interpreted as a market price of risk. Clearly λ, is just the coefficient associated with the systematic risk factor in the APT pricing equation. We shall meet this kind of reasoning again in Chapter 14.

Data From Equation (10.22)

= + BF, r2 = 2 + B2F,