Consider a bond maturing in 18 months, paying semiannual coupons at rate \(5 \%\), with face value \(\$ 10,000\). The term structure is flat, so we identify interest rate \(r\) and yield \(y\), which is \(3 \%\) with continuous compounding. We assume that this rate is subject to an instantaneous shock, characterized by a normal distribution with \(\quad r=0 \%\) and \({ }_{r}=\) \(0.5 \%\), and we want to find V@R at confidence level \(99 \%\).

The current bond price is

 

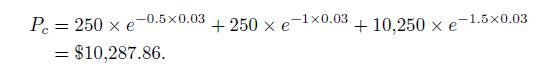
Its duration is

 

The approximated \(\mathrm{V} @ \mathrm{R}\) is given by 

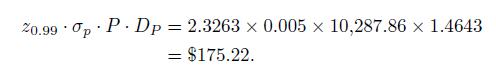
The exact \(\mathrm{V} @ \mathrm{R}\), in this simple case, can be found by just repricing the bond with the worst rate at \(99 \%\) confidence level,

which gives

 

Hence, the exact value-at-risk is 

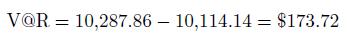
which is fairly close to the approximation.

Transcribed Image Text:

Pe=250 x e-0.5x0.03 +250 x e-1x0.03 +10,250 x e = = $10,287.86. -1.5x0.03