Consider a multi-period economy with dates \(\{0,1, \ldots, T\}\), for some \(T \in \mathbb{N}\), and a time additive utility function of the form:

\[U\left(c_{0}, c_{1}, \ldots, c_{N}\right)=\sum_{t=0}^{T} \delta^{t} u_{t}\left(c_{t}\right)\]

with \(\delta \in(0,1)\) and \(u_{t}: \mathbb{R}_{+} \rightarrow \mathbb{R}\), for all \(t=0,1, \ldots, T\). Let us define by \(r_{u_{t}}^{r}\) the coefficient of relative risk aversion of the utility function \(u_{t}\) (see Sect. 2.2), for all \(t=0,1, \ldots, T\), and define the elasticity of intertemporal substitution of \(U\) as

\[\eta_{U}(s, t):=\frac{\mathrm{d} \log \left(c_{t} / c_{s}\right)}{\mathrm{d} \log \left(\frac{\partial U}{\partial c_{s}} / \frac{\partial U}{\partial c_{t}}\right)}, \quad \text { for all } s, t \in\{0,1, \ldots, T\}\]

Show that the following relation holds for every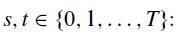  

Moreover, if the utility functions \(\left(u_{t}\right)_{t=0,1, \ldots, T}\) are CRRA with the same coefficient of relative risk aversion for all dates \(t=0,1, \ldots, T\), then it holds that

\[\eta_{U}(s, t)=\frac{1}{r_{u_{t}}^{r}\left(c_{t}\right)}, \quad \text { for all } s, t=0,1, \ldots, T\]

Transcribed Image Text:

s, t {0, 1,..., T}: