(i) Consider the general form of recursive preferences as defined in (9.16). Suppose that the functions (v)...
Question:
(i) Consider the general form of recursive preferences as defined in (9.16). Suppose that the functions \(v\) and \(\tilde{u}\) are of the following form:
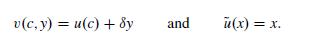
Show that in this case the preference functional (9.16) reduces to the classical time additive utility.
(ii) Consider the recursive utility functional of the Epstein \& Zin [651] form given in (9.19). Show that, if \(\alpha=\varrho\), then the recursive preference functional reduces to the classical time additive expected utility with a power utility function.
Data From Equation (9.16)
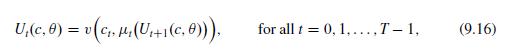
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Financial Markets Theory Equilibrium Efficiency And Information
ISBN: 9781447174042
2nd Edition
Authors: Emilio Barucci, Claudio Fontana
Question Posted:





