In inferential statistics, we learn about the most obvious and desirable property of an estimator: The expected value of the estimator, which is a random variable, should just be the value of the unknown parameter. In such a case, we say that the estimator is unbiased. For instance, it is easy to show that the sample mean is an unbiased estimator of the expected value. However, another feature of an estimator is its variance. If the value of the estimator is too sensitive to the input data, the corresponding instability in estimates may adversely affect the quality of the resulting decisions.

Sometimes, we may reduce variance by accepting a moderate amount of bias. In fact, a relevant issue in statistical modeling is the need to address the bias-variance tradeoff. One example of this idea is the introduction of shrinkage estimators, i.e., estimators that shrink variability by mixing the sample estimate with a fixed value. For instance, the following adjusted estimator of beta has been proposed.

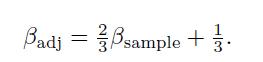
The idea is to take a weighted average between the sample estimate and a fixed value, which in this case is 1 . A unit beta is, in some sense, a standard beta, as it implies that the risk of the asset is just the same as the market portfolio. Furthermore, when firms grow and diversify their lines of business, there is an empirical tendency of beta to move towards 1 .

Transcribed Image Text:

Badj = sample + 13.