Let us consider four assets with the following features: We also have: Therefore, the risk premia are
Question:
Let us consider four assets with the following features:
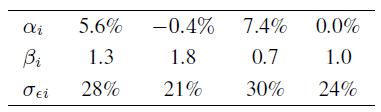
We also have:
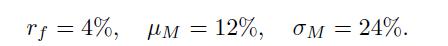
Therefore, the risk premia are

In Step 1, we find the unscaled pseudoweights in the initial portfolio, 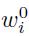 ,
,
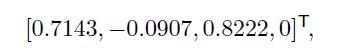
which, after normalization in Step 2, yield the weight \(w_{i}\) of each asset in the active portfolio,
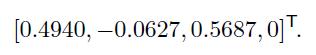
We notice a small short position for the asset with negative alpha, and a zero position for the asset with no specific risk premium. These individual weights are large, but this does not necessarily imply a large final position. The alpha and the residual variance of the active portfolio are calculated as in Step 3:
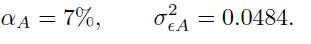
Step 4 yields the "initial" position of the active portfolio,
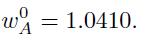
In Step 5 we find its beta,

which is used in Step 6 to find the weight of the active portfolio,
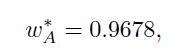
which is fairly large. Then, in the next steps, we find the weight of the index,
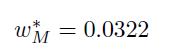
and the weight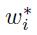 of each asset within the optimal risky portfolio,
of each asset within the optimal risky portfolio,
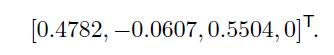
We notice that these weights have been only partially moderated by the index, because of the peculiarity of the data we are using. However, let us see what overall portfolio would an investor with risk aversion \(=4\) choose. We recall from Section 8.1 that the optimal allocation to the risky portfolio is

The risk premium and the variance for the risky portfolio are given by
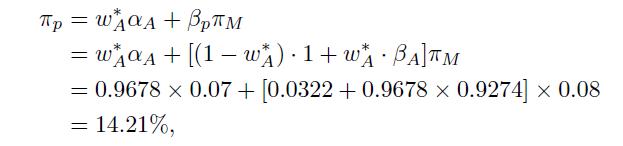
and
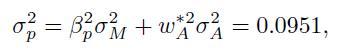
respectively. Therefore, the weights of the risky portfolio and of the risk-free asset are
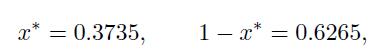
respectively. Then, the actual weight of the index is

and the actual weights of individual assets are given by 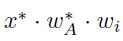 ,
,
which yields
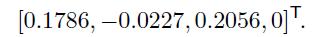
Step by Step Answer:

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte





