Let us consider again an annual percentage rate of (5 %). If we invest ($ 1000), with
Question:
Let us consider again an annual percentage rate of \(5 \%\). If we invest \(\$ 1000\), with no compounding, wealth after one year is
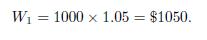
Now, what if interest is earned semiannually? The typical convention is that if the annual rate \(\mathrm{APR}_{2}\) is compounded semiannually, it means that a rate 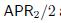 applies to each semester. Hence,
applies to each semester. Hence,
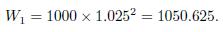
While the quoted rate \(\mathrm{APR}_{2}\) is \(5 \%\), the equivalent effective annual rate \(\mathrm{EAR}_{2}\), with semiannual compounding, is a bit larger and can be found as follows:
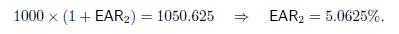
By a similar token, with quarterly compounding we find
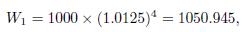
which corresponds to an effective annual rate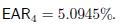
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte
Question Posted:





