Let us consider the prices of three zero-coupon bonds with face value ($ 1000) and different maturities,
Question:
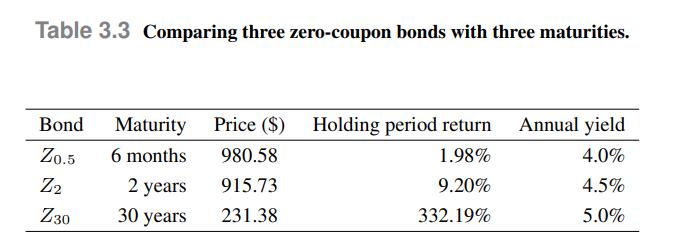
Let us consider the prices of three zero-coupon bonds with face value \(\$ 1000\) and different maturities, as reported in Table 3.3. Given the bond prices, we may compute their annual holding period return, or yield, in other words. For instance, the holding period return for the zero  maturing in 30 years is calculated as
maturing in 30 years is calculated as
![]()
When compared with this seemingly stellar return, the holding period return for the bond \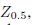 maturing in six months, just pales away. However, it is clear that such a comparison makes no sense at all. We should come up with a common ground for a comparison, and a natural choice is expressing the return on an annual basis. We may invert the pricing formula to find the annual yield on each bond,
maturing in six months, just pales away. However, it is clear that such a comparison makes no sense at all. We should come up with a common ground for a comparison, and a natural choice is expressing the return on an annual basis. We may invert the pricing formula to find the annual yield on each bond,
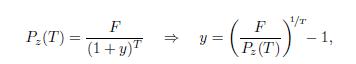
where \(P_{z}(T)\) is the price of a zero-coupon bond maturing in \(T\). Carrying out this calculation gives the last column in Table 3.3. We observe that, indeed, the annualized return on longer maturity bonds is larger, which is usually the case. Plotting interest rates for different maturities provides us with a picture of the term structure of interest rates, as we shall see in Section 3.4, and an increasing structure may be justified by risk considerations. Thus, the return of the long-term bond in Table 3.3 is not really surprising (and just a bit less exciting, when compared with the yields of the other two bonds).
Data From Table 3.3
Step by Step Answer:

An Introduction To Financial Markets A Quantitative Approach
ISBN: 9781118014776
1st Edition
Authors: Paolo Brandimarte





