Suppose that we are going to work for the next \(T\) years, and that at the beginning of each year we contribute an amount \(L\) to a pension fund, which is invested at an annual rate \(r\) for the future time periods (years) until retirement. If annual compounding applies, what is our wealth at retirement?

To formalize the problem, let us introduce time instants (epochs)  We invest money at epochs \(t=0\) through \(t=T \quad 1\), for a total of \(T\) contributions, and we need to evaluate wealth at epoch \(t=T\). The key is that what we contribute at time \(t\) is invested for \(T \quad t\) time periods. As a result, wealth at retirement is

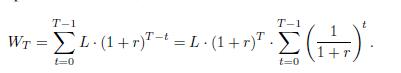
To figure out the sum, we recall a property of the geometric series,

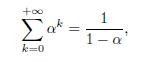
for \(\quad

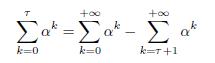
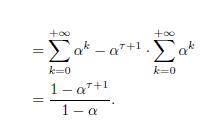
In our case, \[=\frac{1}{1+r}Therefore, we find 

Hence, 

As a quick check, observe that the formula yields \(W_{1}=L \quad(1+r)\) for \(T=1\). For instance, if \(L=\$ 10000, r=5 \%\), and \(T=30\) years, 

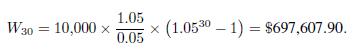
The interest rate has a remarkable impact. If \(r=4 \%\), the above amount drops to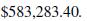  

If simple interest applies, wealth at retirement is 

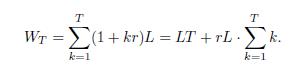
It is easy to see that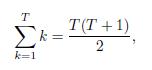 

which implies 

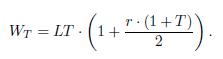
If the above \(5 \%\) rate is applied with no compounding, wealth at retirement is only

 which is less than what we would obtain with \(4 \%\) and compounding.

Transcribed Image Text:

t=0,1,...,T.