Suppose that the economy contains a risk free security paying a constant and deterministic risk free rate
Question:
Suppose that the economy contains a risk free security paying a constant and deterministic risk free rate \(r_{f}>0\). Define the discounted quantities \(\bar{S}_{t}:=S_{t} / r_{f}^{t}\) and \(\bar{D}_{t}:=D_{t} / r_{f}^{t}\), for all \(t=0,1, \ldots, T\). For any trading-consumption strategy \((\theta, c)\), define the discounted portfolio value \(\bar{W}_{t}(\theta):=W_{t}(\theta) / r_{f}^{t}\) and the discounted amount of consumption \(\bar{c}_{t}:=c_{t} / r_{f}^{t}\), for all \(t=0,1, \ldots, T\). Show that the self-financing condition (6.4) is stable with respect to discounting, in the sense that, for any strategy \((\theta,c) \in\mathscr{A}\left(x_{0}\right)\) :
\[\Delta \bar{W}_{t+1}(\theta)=\theta_{t+1}^{\top} \Delta \bar{S}_{t+1}+\theta_{t+1}^{\top} \bar{D}_{t+1}-\bar{c}_{t} .\]
In particular, it holds that
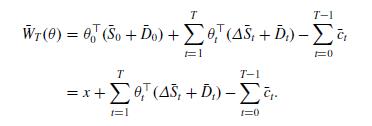
Step by Step Answer:

Financial Markets Theory Equilibrium Efficiency And Information
ISBN: 9781447174042
2nd Edition
Authors: Emilio Barucci, Claudio Fontana





