Suppose that we hold a portfolio of two assets: We have invested \(W_{A}=\$ 10,000\) in stock share \(A\) and \(W_{B}=\$ 20,000\) in stock share \(B\). We assume that daily returns are jointly normal with the following parameters:

where  is the correlation coefficient. We are interested in the daily \(\mathrm{V} @ \mathrm{R}\), so we disregard drift again, with confidence level \(99 \%\).

We first compute the volatility of the holding period return of the whole portfolio:

Therefore

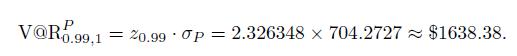
It is interesting to compare the risk of the overall portfolio with the risks of the two individual positions:

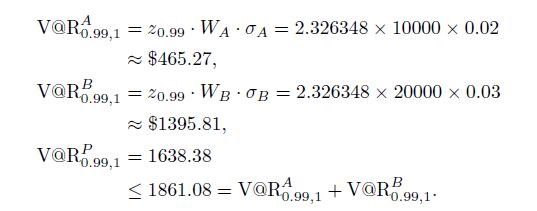
We observe that the risk of the portfolio is less than the sum of the two risks. The amount of this reduction depends on the correlation. The two quantities would be the same for perfect positive correlation, \(=1\), whereas overall risk would be minimized with perfect negative correlation, \(=1\).

Transcribed Image Text:

A = 2%, B=3%, p = 0.4,