We have invested ($100 ),000 in Quacko Corporation stock shares, whose daily volatility is (2 ) This means that the volatility of asset return is where the holding period (H ) is one day and (R H ) is the daily return For the sake of simplicity, let us assume that the return is normally distributed...

The Answer is in the image, click to view ...

We have invested ($100),000 in Quacko Corporation stock shares, whose daily volatility is (2 %). This means

Question:

We have invested $$100$,000 in Quacko Corporation stock shares, whose daily volatility is $2 \%$. This means that the volatility of asset return is

image text in transcribed

where the holding period $H$ is one day and $R_{H}$ is the daily return. For the sake of simplicity, let us assume that the return is normally distributed. Given the square-root rule, 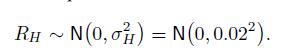image text in transcribed

Loss over the holding period is \[L_{H}=W_{0} R_{H}\]
where the initial wealth $W_{0}$ is $\$ 100,000$. The expected value of loss is $\mathrm{E}\left[L_{H}\right]=0$, and its volatility is \[{ }_{L}=\overline{\operatorname{Var}\left(L_{H}\right)}=\overline{\left(W_{0}\right)^{2} \quad \operatorname{Var}\left(R_{H}\right)}=W_{0} \quad H\]
We know that quantiles of a normal distribution are related to quantiles $z_{1} \quad$ of a standard normal variable. If we want daily V $@ \mathrm{R}$ with $99 \%$ confidence level, we find

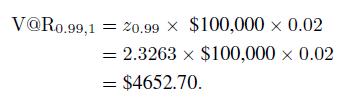
image text in transcribed