We know from the Normal tables that for a standard Normal density, prob (z >

1.96) = 0.025. Because the Normal density is symmetric, we can also say that prob (z

Assume that the distribution of a sample mean x is Normal with mean m and variance s2. Use the standard Normal limits above to claim: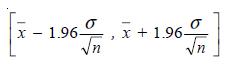

Suppose you could repeatedly draw samples of size n and compute the mean of each such sample. Then 95% of the time, the interval will contain the true mean m. The above interval is said to be a 95% confidence interval for m.
Loosely speaking, once we have computed the sample mean 0 we can be 95%
confident that the true mean will lie between the two limits.
Getting back to our debate with Thomas, let’s look at this another way. We draw a sample of size four, and find a sample mean of 1.1%. We know the population standard deviation is s = 2%.
(i) Find a 95 % confidence limits for the population mean of stock returns.
(ii) Now change the sample size to n = 100. What happens to the confidence limits?

x 1.96- -1.96 x+1.96- n