In the case of a two-dimensional system that is not almost linear, the trajectories near an isolated critical point can exhibit a considerably more complicated structure than those near the nodes, centers, saddle points, and spiral points discussed in this section. For example, consider the system

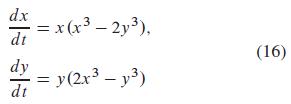
having (0, 0) as an isolated critical point. This system is not almost linear because (0, 0) is not an isolated critical point of the trivial associated linear system x' = 0, y' = 0. Solve the homogeneous first-order equation

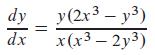
to show that the trajectories of the system in (16) are folia of Descartes of the form

where c is an arbitrary constant (Fig. 9.2.14).

Transcribed Image Text:

dx = x(x² - 2y²), dt dy dt = y(2x² - y²) (16)