The term bifurcation generally refers to something splitting apart. With regard to differential equations or systems involving
Question:
The term bifurcation generally refers to something “splitting apart.” With regard to differential equations or systems involving a parameter, it refers to abrupt changes in the character of the solutions as the parameter is changed continuously. Problems 33 through 36 illustrate sensitive cases in which small perturbations in the coefficients of a linear or almost linear system can change the type or stability (or both) of a critical point.
Consider the linear system
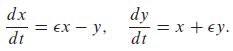
Show that the critical point (0,0) is
(a) A stable spiral point if ϵ < 0;
(b) A center if ϵ = 0;
(c) An unstable spiral point if ϵ > 0. Thus small perturbations of the system x' = -y, y' = x can change both the type and stability of the critical point. Figures 9.2.13(a)-(e) illustrate the loss of stability that occurs at ϵ = 0 as the parameter increases from ϵ < 0 to ϵ > 0.
Figures 9.2.13(a)-(e)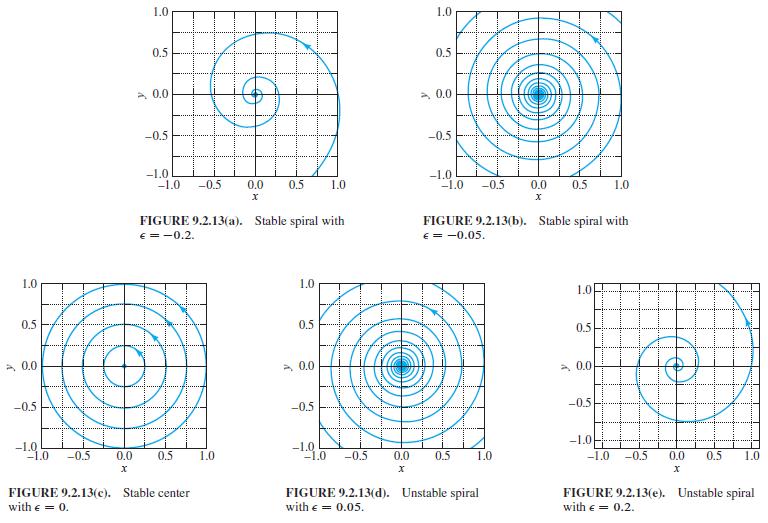
Step by Step Answer:

Differential Equations And Linear Algebra
ISBN: 9780134497181
4th Edition
Authors: C. Edwards, David Penney, David Calvis





