When all the curves in a family G(x, y, c 1 ) = 0 intersect orthogonally all
Question:
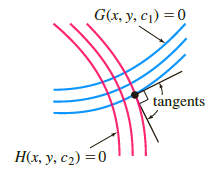
y = c1x
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

A First Course in Differential Equations with Modeling Applications
ISBN: 978-1305965720
11th edition
Authors: Dennis G. Zill
Question Posted:





