Consider the steady, incompressible, two-dimensional flow field of Prob. 4–64. Using the results of Prob. 4–64(a), do the following:

(a) From the fundamental definition of the rate of rotation (average rotation rate of two initially perpendicular lines that intersect at a point), calculate the rate of rotation of the fluid particle in the xy-plane, ω_z.

(b) Compare your results with those obtained from the equation for ω_z in Cartesian coordinates, i.e.,

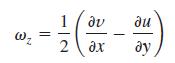
Data from Problem 64(a)

Consider steady, incompressible, two-dimensional shear flow for which the velocity field is

where a and b are constants. Sketched in Fig. P4–64 is a small rectangular fluid particle of dimensions dx and dy at time t. The fluid particle moves and deforms with the flow such that at a later time (t + dt), the particle is no longer rectangular, as also shown in the figure. The initial location of each corner of the fluid particle is labeled in Fig. P4–64. The lower-left corner is at (x, y) at time t, where the x-component of velocity is u = a + by. At the later time, this corner moves to (x + u dt, y), or (x + (a + by) dt, y)

(a) In similar fashion, calculate the location of each of the other three corners of the fluid particle at time t + dt.

Transcribed Image Text:

Cz 1 ду 2 Әх ди ду