Consider steady, incompressible, two-dimensional shear flow for which the velocity field is

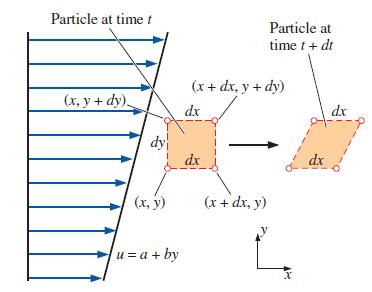
where a and b are constants. Sketched in Fig. P4–64 is a small rectangular fluid particle of dimensions dx and dy at time t. The fluid particle moves and deforms with the flow such that at a later time (t + dt), the particle is no longer rectangular, as also shown in the figure. The initial location of each corner of the fluid particle is labeled in Fig. P4–64. The lower-left corner is at (x, y) at time t, where the x-component of velocity is u = a + by. At the later time, this corner moves to (x + u dt, y), or (x + (a + by) dt, y)

(a) In similar fashion, calculate the location of each of the other three corners of the fluid particle at time t + dt.

(b) From the fundamental definition of linear strain rate (the rate of increase in length per unit length), calculate linear strain rates ε_xx and ε_yy.

(c) Compare your results with those obtained from the equations for ε_xx and ε_yy in Cartesian coordinates, i.e.,

Transcribed Image Text:

V = (u, v) = (a + by)i + 07