Converging duct flow is modeled by the steady, two dimensional velocity field of Prob. 417. A fluid
Question:
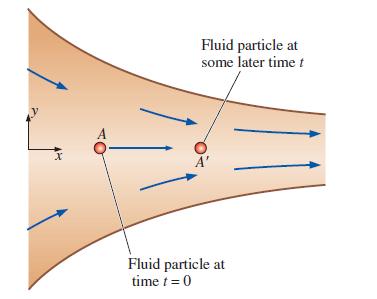
Converging duct flow is modeled by the steady, two dimensional velocity field of Prob. 4–17. A fluid particle (A) is located on the x-axis at x = xA at time t = 0 (Fig. P4–51).
At some later time t, the fluid particle has moved downstream with the flow to some new location x = xA´, as shown in the figure. Since the flow is symmetric about the x-axis, the fluid particle remains on the x-axis at all times. Generate an analytical expression for the x-location of the fluid particle at some arbitrary time t in terms of its initial location xA and constants U0 and b. In other words, develop an expression for xA´.
Data from Problem 17.
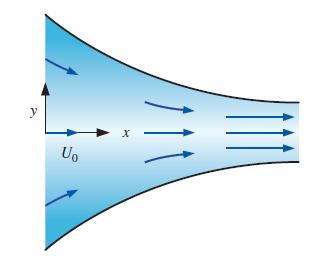
Consider steady, incompressible, two-dimensional flow through a converging duct (Fig. P4–17). A simple approximate velocity field for this flow is
![]()
where U0 is the horizontal speed at x = 0. Note that this equation ignores viscous effects along the walls but is a reasonable approximation throughout the majority of the flow field. Calculate the material acceleration for fluid particles passing through this duct. Give your answer in two ways:
(1) As acceleration components ax and ay
(2) As acceleration vector a(vector)
Step by Step Answer:

Fluid Mechanics Fundamentals And Applications
ISBN: 9781259696534
4th Edition
Authors: Yunus Cengel, John Cimbala





