Oftentimes it is desirable to work with an established dimensionless parameter, but the characteristic scales available do not match those used to define the parameter. In such cases, we create the needed characteristic scales based on dimensional reasoning (usually by inspection). Suppose for example that we have a characteristic velocity scale V, characteristic area A, fluid density ρ, and fluid viscosity μ, and we wish to define a Reynolds number. We create a length scale L = √A, and define

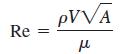
In similar fashion, define the desired established dimensionless parameter for each case: 

(a) Define a Froude number, given V̇´ = volume flow rate per unit depth, length scale L, and gravitational constant g. 

(b) Define a Reynolds number, given V̇´ = volume flow rate per unit depth and kinematic viscosity n. 

(c) Define a Richardson number (see Table 7–5), given V̇´ = volume flow rate per unit depth, length scale L, characteristic density difference Δρ, characteristic density ρ, and gravitational constant g.

Data from table 7-5

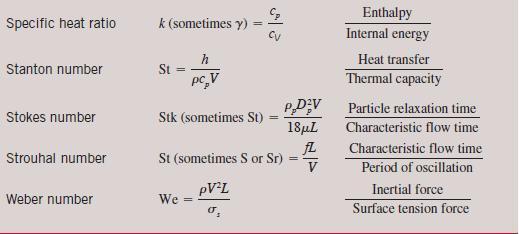
Re = PVVA