Question: The outer product of two vectors is a second-order tensor with nine components. In Cartesian coordinates, it is The product rule applied to the divergence

The outer product of two vectors is a second-order tensor with nine components. In Cartesian coordinates, it is

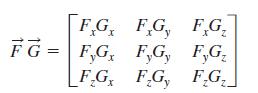
FG FG FG FG= F,G, F,G, F,G FG FG FG

The product rule applied to the divergence of the product of two vectors F(vector) and G(vector) is written as

Expand both sides of this equation in Cartesian coordinates and verify that it is correct.

FG FG FG FG= F,G, F,G, F,G FG FG FG

Step by Step Solution

★★★★★

3.43 Rating (166 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Fluid Mechanics Questions!

Q:

Step 3: Hypothesis Test for the Population Mean (I) A relative skill level of 1340 represents a critically low skill level in the league. The management of your team has hypothesized that the average...

Q:

Use the product rule of Prob. 911 to show that Data from Problem 11 The outer product of two vectors is a second-order tensor with nine components. In Cartesian coordinates, it is The product rule...

Q:

The cross product of the vectors is the vector computed as this determinant. The first row's entries are vectors, the vectors from the standard basis for R3. Show that the cross product of two...

Q:

On September 1, 201X, Dan Potter opened an auto repair shop. Here is his chart of accounts: Assets Liabilities Equity 101 Cash 201 Accounts Payable 301 Dan Potter, Capital 102 Accounts Receivable 302...

Q:

Calculus 3 Section 12.4 Reading Assignment: The Cross Product Answer Only Exercise 1 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very carefully...

Q:

Calculus 3 Section 12.4 Reading Assignment: The Cross Product Answer Only Exercise 1 by using a screenshot provided Calculus Pearson textbook. Make sure you read these three questions very carefully...

Q:

10 Green's functions for PDEs In this final chapter we will apply the idea of Green's functions to PDEs, enabling us to solve the wave equation, diffusion equation and Laplace equation in unbounded...

Q:

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Q:

supporting examples: 6-4. Normal Viscous Stress at a Solid Surface The objective is to show that the normal component of the viscous stress vanishes at a solid surface. This is true for solids of any...

Q:

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

Q:

1. Compute the year-to-year percentage change in "diluted-income from continuing operations" for each of the five years. 1a. Do the earnings appear volatile? 2. Compute the ratio of long term debt to...

Q:

a) if 0 = 50 and F = 30 kN, determine the magnitude of the resultant force and its direction measured clockwise from the positive x axis. Show detailed calculations. 50 kN V2 40 kN b) What is the...

Q:

In 2019, Jason Jones, a director of MeatInTheBox met Cameron Charles, the owner and executive chef of TrendFoods, at a party in Balmain. Cameron was fascinated to learn that Jasons family had some...

Q:

Which types of insurance is available to disabled Americans? . Medicare, Medicaid Private Blue Cross Employer based

Q:

Ruby had to package 1575 calculators in the production line of a factory. If she was able to package 75 calculators in two hours and her hourly rate is $30, calculate her earnings for that work....

Q:

Repeat Prob. 1542, except for several values of the Mach number, ranging from 1.10 to 3.0. Plot the calculated Mach angle as a function of Mach number and compare to the theoretical Mach angle (Chap....

Q:

Repeat Prob. 1542, except for several values of the Mach number, ranging from 1.10 to 3.0. Plot the calculated Mach angle as a function of Mach number and compare to the theoretical Mach angle (Chap....

Q:

Paul realizes that the pump being used in Prob. 1439E is not well-matched for this application, since its shutoff head (125 ft) is much larger than its required net head (less than 30 ft), and its...

Q:

CASE # 1 (Managing without Managers) Just Music, a European commercial music service, is synonymous with dramatically changing the way consumers access and use music on a day-to-day basis. They have...

Q:

Please answer the following questions using at least 5 sentences. Thanks 1. What are some examples of corporate culture that might lead to employee fraud? 2. Describe big bath accounting and what...

Q:

At what point in time does a governmental fund report an expenditure