FREE Trial

Verify that the spiraling line vortex/sink flow in the r-plane of Prob. 917 satisfies the two-dimensional incompressible continuity equation. What

Question:

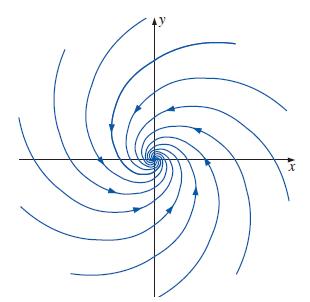
Verify that the spiraling line vortex/sink flow in the rθ-plane of Prob. 9–17 satisfies the two-dimensional incompressible continuity equation. What happens to conservation of mass at the origin? Discuss.


Data from Problem 17

Consider a spiraling line vortex/sink flow in the xy-or rθ-plane as sketched in Fig. P9–17. The two-dimensional cylindrical velocity components (ur, uθ) for this flow field are ur = C/2πr and uθ = Γ/2pr, where C and G are constants (m is negative and Γ is positive). Transform these two-dimensional cylindrical velocity components into two dimensional Cartesian velocity components (u, v). Your final answer should contain no r or θ—only x and y. As a check of your algebra, calculate V2 using Cartesian coordinates, and compare to V2 obtained from the given velocity components in cylindrical components.


Figure 9-17

Transcribed Image Text:

X

This problem has been solved!


Do you need an answer to a question different from the above? Ask your question!

Step by Step Answer:

Answer rating: 33% (3 reviews)

To verify that the spiraling line vortex sink flow in the r plane of Prob 917 satisfies the two dime…View the full answer


answer-question
Answered By
tutor-profile-image
User l_998468
I have extensive tutoring experience, having worked as a private tutor for over three years. I have tutored students from different academic levels, including high school, undergraduate, and graduate levels. My tutoring experience has taught me to be patient, attentive to student needs, and effective in communicating difficult concepts in simple terms. I have a strong background in statistics, probability theory, data analysis, and data visualization. I am proficient in using statistical software such as R, Python, and SPSS, which are commonly used in academic research and data analysis. Additionally, I have excellent communication and interpersonal skills, which enable me to establish rapport with students, understand their learning styles, and adapt my teaching approach to meet their needs. I am passionate about teaching and helping students achieve their academic goals.
0.00 0 Reviews 10+ Question Solved
Related Book For  answer-question
Fluid Mechanics Fundamentals And Applications

Fluid Mechanics Fundamentals And Applications

ISBN: 9780073380322

3rd Edition

Authors: Yunus Cengel, John Cimbala

See More Books
Question Details
Chapter # 9- DIFFERENTIAL ANALYSIS OF FLUID FLOW
Section: Problems
Problem: 26
View Solution
Create a free account to access the answer
Cannot find your solution?
Post a FREE question now and get an answer within minutes. * Average response time.
Question Posted: September 16, 2023 23:36:15
See More Questions

Students also viewed these Engineering questions

Q:
Consider a spiraling line vortex/sink flow in the xy-or r-plane as sketched in Fig. P917. The two-dimensional cylindrical velocity components (ur, u ) for this flow field are u r = C/2r and u =...
A:
To transform two dimensional cylindrical velocity components ur u into two dimensional Cartesian vel......
Q:
The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...
A:
1040 of the sury Internal Reverse Service For the year Jan 1 Dec 31 2012 or other tax your beginning Your first name and initial Ivan 1 If a joint return spouse s first name and initial Incisor Irene......
Q:
You are CFO of a large company that has a few subsidiaries. A new board member is unfamiliar with consolidation procedures particularly with respect to the elimination of intercompany inventory...
A:
Parent and Subsidiary transactions should are viewed as internal transactions of a single economic a......
Q:
Because of excessive pollution on the Momiss River, the state of Momiss is going to build pollution control stations. Three sites (1, 2, and 3) are under consideration. Momiss is interested in...
A:
Consider the Integer Programming problem of population control in Momiss River The State Legislator......
Q:
A stock has an expected return of 16.2%, a beta of 1.75, and the expected return on the market is 11 percent. What must the risk-free rate be?
A:
Computation of the Risk Free Rate E r R f......
Q:
Chemet manufactures chemicals in a continuous process. The company combines various materials in a specially configured machine at the beginning of the process, and conversion is considered uniform...
A:
Inspection Inspection Inspection at 20 at 45 at 100 Work in process beginning 25 Started during......
Q:
How are selfgenerated intangible assetsbrand and goodwillaccounted for?
A:
Self generated intangible assets such as brand and goodwill are not recognized as assets on a company s balance sheet under generally accepted account......
Q:
On January 1, 2010, the Baznik Company adopted a defined benefit pension plan. At that time, the company awarded retroactive benefits to certain employees. These retroactive benefits resulted in a...
A:
Number of Service Years Expected Years of Rendered in Each Year 1 a Employee Future Service 2010 201......
Q:
How does being exposed to financial literacy while younger could potentially increase net worth in the future? List some ways.
A:
I Exposure to financial literacy at a young......
Q:
Verify that the steady, two-dimensional, incompressible velocity field of Prob. 916 satisfies the continuity equation. Stay in Cartesian coordinates and show all your work. Data from Problem 16 A...
A:
To verify that the given velocity field satisfies the continuity equation in Cartesian coordinates w......
Q:
In Example 96 we derive the equation for volumetric strain rate, Write this as a word equation and discuss what happens to the volume of a fluid element as it moves around in a compressible fluid...
A:
Click to View...
Q:
Singh Company produces two products: a mostly handcrafted soft leather briefcase sold under the label Elegant and a leather briefcase produced largely through automation and sold under the label...
A:
1 Yes Because direct materials and direct labour are directly traceable to each product their cost a......
Q:
A gas turbine powerplant is intaking 10 L/s of air at sea level (1 atm) with the density of 1.1 kg/m3. Compression ratio in compressor is 30:1. Kerosine is used as the fuel with the calorific value...
A:
Given Data Air intake air 10L sVair 10L s Air density air 1 1kg m3air 1 1kg m3 Compression ratio CR......
Q:
Lila Thompson is a remarkable 58-year-old marine biologist with a lifelong passion for exploring and preserving the delicate ecosystems of the California coast. Hailing from the vibrant city of San...
A:
1 To determine which of Lila s retirement plans would allow her to take a penalty free withdrawal of 25 000 for her vacation we need to consider the different account types and their withdrawal rules......
Q:
6. One readily accessible source for generic job descriptions is? 7. a. Bureau of National Affairs b. Department of Labor c. Occupational Information Network d. Dictionary of Occupational Titles...
A:
The detailed answer for the above question is provided below Quiz 6 Correct answer c Occupational In......
Q:
Write about the types of time perceptions which are given below ,Explain in details 1. Circular perception 2. Linear perception 3. Time as a resource 4. Procedural perception 5. Activity based...
A:
The detailed answer for the above question is provided below 1 Circular Perception Definition Circular perception of time is rooted in cyclic patterns......
Q:
Julio has a businessrepairing bicycles and he operates from his garage at home. He is getting somuch business he decides to rent a small workshop in North Hobart. He signs a six-month lease with...
A:
Julio is subject to the conditions of the six month lease which provide that rent is due on the tent......
Q:
List any errors you can find in the following partial balancesheet: JENNETT COMPANY Balance Sheet December 31, 2010 Assets Current assets: Cash Notes receivable Less interest receivable Account...
A:
1 The interest receivable should be reported separately as a current asset It should not be de......
Q:
Review Exhibit 11.4. Analyze each product on the graph according to the characteristics that influence the rate of adoption. For example, what can you conclude from the data about the relative...
A:
For example one can conclude from the graph that the tremendous success of cell phones can......
Q:
FIGURE EX17.28 shows the circular wave fronts emitted by two wave sources. a. Are these sources in phase or out of phase? Explain. b. Make a table with rows labeled P, Q, and R and columns labeled r...
A:
Solve a The circular wave fronts emitted by the two sources indicate the sources are out......
Q:
A very thin oil film (n = 1.25) floats on water (n = 1.33). What is the thinnest film that produces a strong reflection for green light with a wavelength of 500 nm?
A:
Model Reflection is maximized if the two reflected waves interfere constructively S......
Q:
What is the thinnest film of MgF 2 (n = 1.39) on glass that produces a strong reflection for orange light with a wavelength of 600 nm?
A:
Model Reflection is maximized if the two reflected waves interfere constructively S......
The Automation Of The Clinical Practice Lessons In Systems Management 1st Edition - ISBN: 154277019X - Free Book