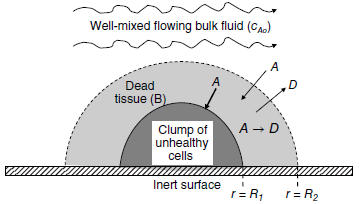
Consider the drug treatment system shown in the figure below. A hemispherical cluster of unhealthy cells is surrounded by a larger hemisphere of stagnant dead tissue (species B), which is turn surrounded by a flowing fluid. The bulk, wellmixed fluid contains a drug compound (species A) of constant but dilute bulk concentration c_Ao. Drug A is also soluble in the unhealthy tissue but does not preferentially partition into it relative to the fluid. The drug (species A) enters the dead tissue and targets the unhealthy cells. At the unhealthy cell boundary (r = R₁), the consumption of drug A is so fast that the flux of A to the unhealthy cells is diffusion limited. All metabolites of drug A produced by the unhealthy cells stay within the unhealthy cells. However, drug A can also degrade to inert metabolite D by a first-order reaction dependent on c_A€”i.e., A A^k†’D€”that occurs only within the stagnant dead tissue.

a. State all reasonable assumptions and conditions that appropriately describe the system for mass transfer.

b. Develop the differential form of Fick€™s flux equation for drug A within the multicomponent system without the €œdilute system€ assumption. Then, simplify this equation for a dilute solution. State all additional assumptions as necessary.

c. Appropriately simplify the general differential equation for mass transfer for drug A. Specify the final differential equation in two ways: in terms of N_A, and in terms of concentration c_A.

d. Specify the boundary conditions for both components A and D.

Transcribed Image Text:

Well-mixed flowing bulk fluid (CA.) A Dead tissue (B). A - D Clump of unhealthy cells Inert surface r= R2 r= R1