Consider the physical system shown in the figure on page 532. which represents a simplified scenario for
Question:
a. Define the system for mass transfer of drug A, the source for drug A, and the sink(s) for drug A. Propose five reasonable assumptions for this process.
b. Based on a material balance on a differential volume element of the system for drug A. develop a differential equation for CA(z) in the healthy tissue layer.
c. State the boundary conditions that accurately describe the physical system and allow for a mathematical analysis of the diffusion process developed in part (b).
d. Develop an analytical model, in final integrated form, to predict CA(z). Your final model should have the following terms in it: CAˆž, NA.s, DAe, K, k1, L, z; CAo and CAs should not be terms in the final model.
e. Refer the process model input parameters below. What is the total therapeutic drug delivery rate delivered to the tissue (NA,o at z = 0) in units of mg/cm2-day?
Process input parameters: Concentration of drug A in liquid medium. cAˆž = 3.0 mg/cm3; partitioning constant between liquid medium and healthy tissue, K = 0.1 cm3 tissue/cm3 liquid; diffusion coefficient of drug A in healthy tissue, DAe = 1.0 · 10-5 cm2/s; rate constant for degradation of drug A in healthy tissue, k1 = 4.0 · 10-5 s-1; thickness of healthy tissue layer, L = 0.5 cm; target therapeutic flux rate of drug A into tumor at z = L, NA,s = 2.0 · 10-6 mg/cm2-s.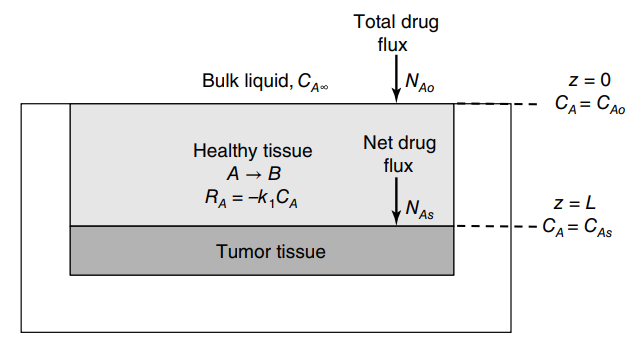
Step by Step Answer:

Fundamentals Of Momentum Heat And Mass Transfer
ISBN: 9781118947463
6th Edition
Authors: James Welty, Gregory L. Rorrer, David G. Foster





