A horizontal flow initially at Mach 1 flows over a downward-sloping expansion corner, thus creating a centered

Question:

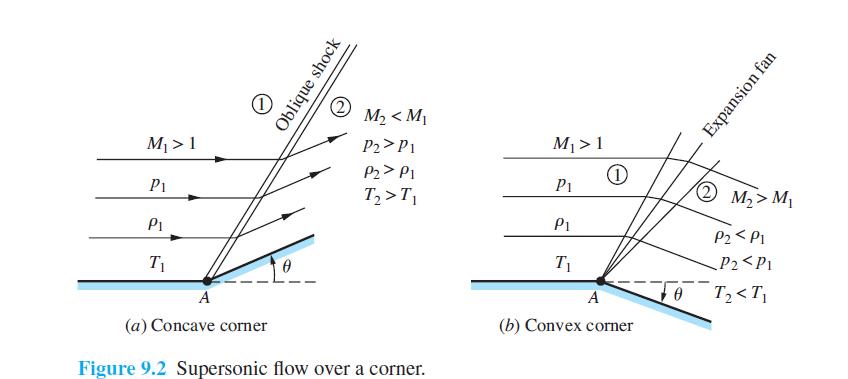
A horizontal flow initially at Mach 1 flows over a downward-sloping expansion corner, thus creating a centered Prandtl-Meyer expansion wave. The streamlines that enter the head of the expansion wave curve smoothly and continuously downward through the expansion fan, and emerge parallel to the downward sloping surface downstream of the tail of the wave, as shown in Figure 9.2b. Imagine a polar coordinate system r ,Ф with its origin at the expansion corner (the vertex of the Prandtl- Meyer expansion wave), with r the usual radial distance along a ray from the origin and Ф the polar angle of r measured from the horizontal. Because the upstream flow is at Mach 1, the head of the expansion fan is a Mach wave perpendicular to the free stream. Consider a given streamline entering the expansion wave at the point (r ,Φ) = (r ∗, π/2). Construct a method for calculating the shape of this streamline as a function of r and Φ through the expansion fan.