The Hirschfelder-Bird-Spotz equation is commonly used in predicting binary bas diffusivities by using its theoretical foundations. A
Question:
The Hirschfelder-Bird-Spotz equation is commonly used in predicting binary bas diffusivities by using its theoretical foundations. A more recent correlation has been developed by Fuller and is given as:
\[D_{A B}=\frac{101.3 T^{1.75}\left(\frac{1}{M_{A}}+\frac{1}{M_{B}}\right)^{1 / 2}}{P\left[\left(\sum V_{A}\right)^{1 / 3}+\left(\sum V_{B}\right)^{1 / 3}\right]^{2}}\]
Where:
\[\begin{aligned}& P=\text { total pressure }(\mathrm{Pa}) \\& M_{i}=\text { molecular weight of species, } i \\& D_{A B}=\text { diffusivity, } \mathrm{cm}^{2} / \mathrm{s} \\& T=\text { temperature, } \mathrm{K}\end{aligned}\]
\(\sum V_{i}=\) Sum of the diffusion volumes for component \(i\), as given in the Table P3.27 Calculate the diffusivity of \(\mathrm{CH}_{4}\) in air at \(35^{\circ} \mathrm{C}\) at \(1 \mathrm{~atm}\).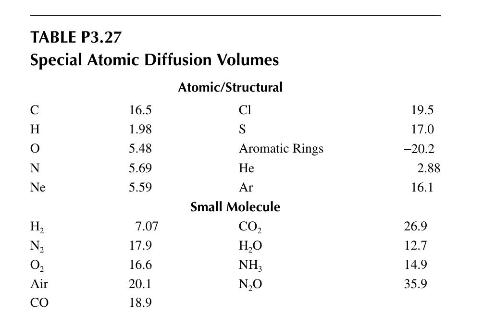
Step by Step Answer:






