Using the results of Free Volume theory for calculating the viscosity of liquids, determine \(\Delta G^{\dagger}\) for the following liquids \(\left(20^{\circ} \mathrm{C})\) : water, ethylene glycol, refrigerant \(134 \mathrm{a}\), and engine oil. Is there any relationship between their molecular structure and interactions and \(\Delta G^{\dagger}\) ?

Transcribed Image Text:

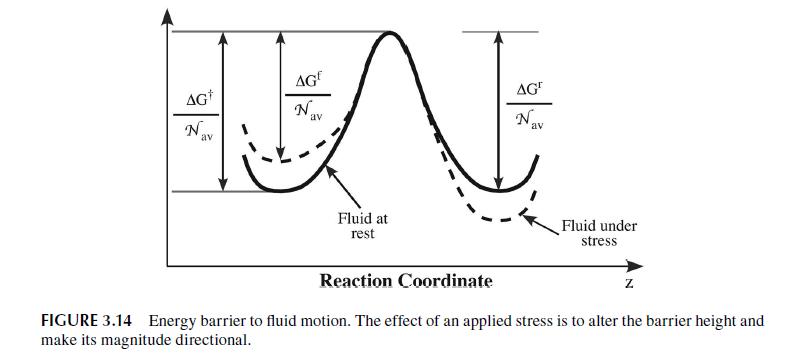
3.6 VISCOSITY OF LIQUIDS-FREE VOLUME THEORY The example calculation we performed in the previous section showed that we have a good theo- retical understanding of the molecular basis for gas viscosity. Our understanding of the viscosity of liquids is largely empirically based. Molecular dynamics calculations have greatly improved the situation, but a simple kinetic theory of liquids is not available since we cannot calculate, in any analytical way, the extent of the intermolecular interactions in dense systems such as liquids. Still, a number of theories of liquid viscosity have been developed and it is instructive to consider one of the more successful: the phenomenological, rate-based model originally developed by Henry Eyring and coworkers during the 1940s and 1950s that is similar to the model we used to estimate the dif- fusivity in a liquid. This model has been extended to a generalized model called the free volume or rate model [16,17]. The particles of a pure liquid at rest are in a constant state of motion similar to a gas. Since the particles are so closely packed, the motion is largely vibrational in scope and limited to a cage- like area formed by the nearest neighbor particles. The situation is shown in Figure 3.13 where the vacant sites, or holes, are referred to as free volume. This free volume may redistribute itself throughout the liquid, requiring no energy to do so. Eventually free volume collects to form a space