The cash flows on the car loan are in annuity form, so we only need to find the payment. The interest rate is 15%/12 = 1.25% per month, and there are 72 months. The first thing we need is the annuity factor for 72 periods at 1.25 percent per period:

Your payment is just under \($400\) per month.
The actual interest rate on this loan is 1.25 percent per month. Based on our work in the chapter, we can calculate the effective annual rate as:

The effective rate is about one point higher than the quoted rate.
To determine the loan balance in two years, we could amortize the loan to see what the balance is at that time. This would be fairly tedious to do by hand.
Using the information already determined in this problem, we can instead simply calculate the present value of the remaining payments. After two years, we have made 24 payments, so there are 72 - 24 = 48 payments left. What is the present value of 48 monthly payments of \($399.64\) at 1.25 percent per month?
The relevant annuity factor is:

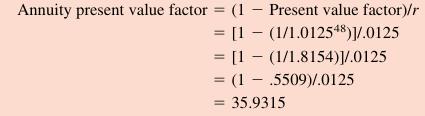
The present value is thus:
Present value = \($399.64\) × 35.9315 = \($14,359.66\) You will owe about \($14,360\) on the loan in two years.

Transcribed Image Text:

Annuity present value factor = - (1 Present value factor)/r = [1 = [1 (1/1.012572)]/.0125 (1/2.4459)]/.0125 = (1.4088)/.0125 = 47.2925 The present value is the amount we finance. With a 10 percent down payment, we will be borrowing 90 percent of $21,000, or $18,900. So, to find the pay- ment, we need to solve for C in the following: $18,900 CX Annuity present value factor = C X 47.2925 Rearranging things a bit, we have: C $18,900 x (1/47.2925) = $18,900 x .02115 = = $399.64