(a) In order to solve the diffusion equation by the method of separation of variables, let and...
Question:
(a) In order to solve the diffusion equation
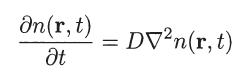
by the method of separation of variables, let
![]()
and show that
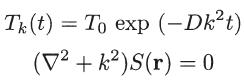
where k2 is the separation constant and T0 is a constant.
(b) Assuming that S depends only on the x coordinate, show that
![]()
where k can be either positive or negative, and that
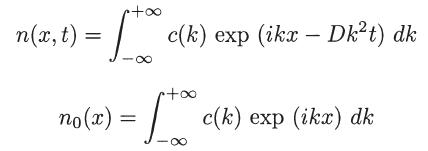
where n0(x) = n(x, 0) is the known initial density distribution.
(c) Using Fourier transform theory, show that
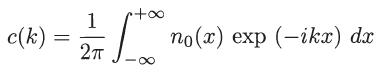
and, consequently, that
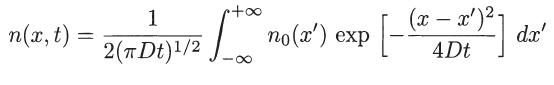
(d) Taking as initial condition
![]()
show that
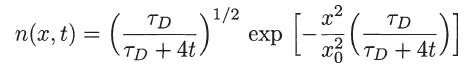
where τD = x02/D is a characteristic time for diffusion to smooth out the density n.
(e) Generalize the problem for the three-dimensional case in Cartesian coordinates, when S = S(r).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





