Consider a gas mixture of two types of particles ( = 1, 2), each one characterized by
Question:
Consider a gas mixture of two types of particles (α = 1, 2), each one characterized by a Maxwellian distribution function
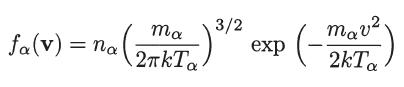
with its own mass, density, and temperature.
(a) Make the following transformation of velocity variables,
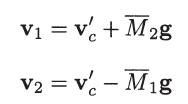
where v′c is a velocity similar to the center of mass velocity, g is the relative velocity between the two species (g = v1 – v2), and
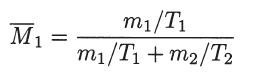
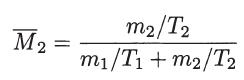
Show that the Jacobian of this transformation,
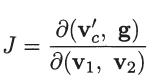
satisfies |J| = 1, so that d3v′c d3g = d3v1 d3v2 .
(b) The relative speed between the two species, g = |v1 – v2|, when averaged over both their velocity distribution functions, is given by
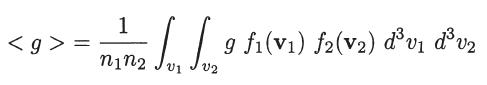
Transform the variables of integration v1 and v2 to v′c and g, and perform the integrals over v′c and g to show that
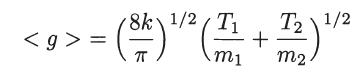
(c) If only one kind of particle is present, so that m1 = m2 = m, T1 = T2 = T, and n1 = n2 = n, show that
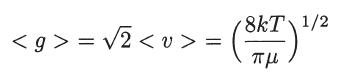
where < v > = (8kT/πm)1/2 is the average speed and μ = m/2 is the reduced mass. If the mutual scattering cross section is a, show that the collision frequency in a homogeneous Maxwellian gas is given by
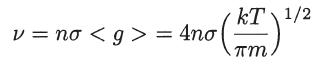
Step by Step Answer:






