Consider the following expressions that define the Fokker-Planck coefficients of dynamic friction and of diffusion in velocity
Question:
Consider the following expressions that define the Fokker-Planck coefficients of dynamic friction and of diffusion in velocity space:
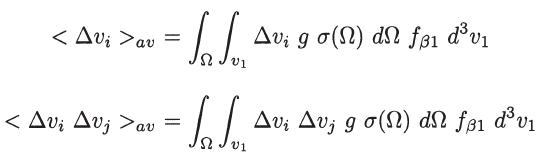
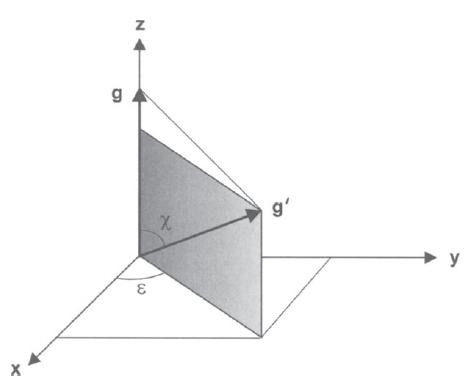
(a) With reference to Fig. 6, verify that

For a general inverse-power interparticle force of the form
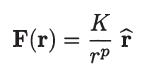
where K is a constant and p is a positive integer number, show that [see (5.18)]
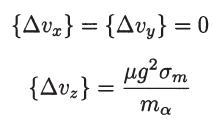
where μ is the reduced mass and σm is the momentum transfer cross section given by
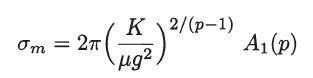
where
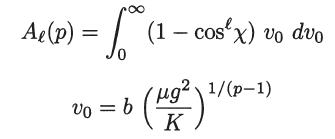
Verify also that [see (5.19)]
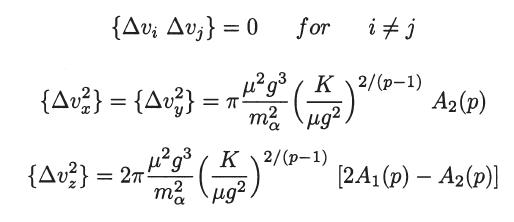
(b) For the case of Maxwell molecules (p = 5), where the results are independent of fβ1, show that the Fokker-Planck coefficients are given by
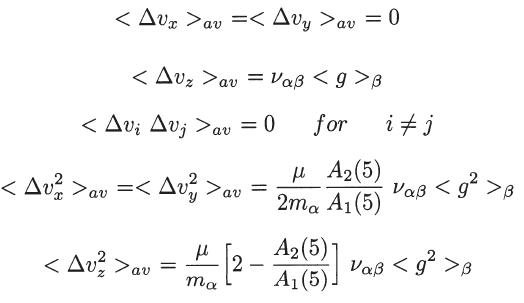
where
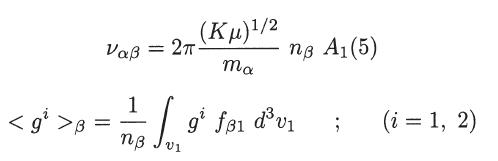
(c) Calculate the Fokker-Planck coefficients for the case of the coulomb interaction (p = 2) using the results of part (a) and of problem 20.6, in terms of integrals over fβ1.
(d) Calculate the Fokker-Planck coefficients for electron-electron interactions, when fβ1 is the Maxwellian distribution function. Refer to (5.49), (5.50), and (5.51).
Figure 6.
Equations
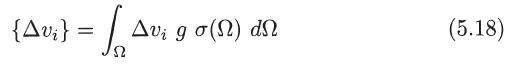
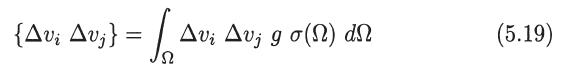

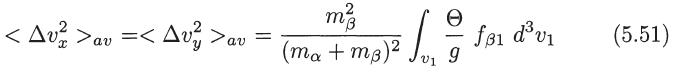
Data from problem 20.6.
Show that for the case of coulomb interactions (p = 2) we have
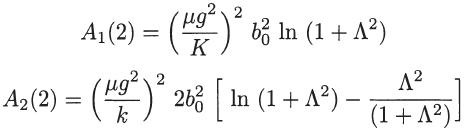
where b0 = qq1/(4π∈0μg2), Aℓ(p) is as defined, and A = λD/b0. For ∧ ≫ 1 verify that
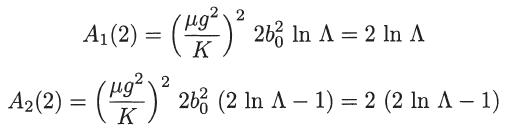
Note that, since K = qq1/(4π∈0) for the coulomb interaction potential, we have (μg2/K)2 b02 = 1.
Step by Step Answer:






