Show that for the case of coulomb interactions (p = 2) we have

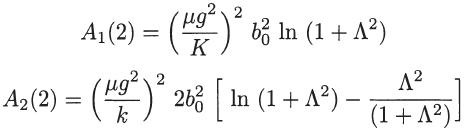
where b₀ = qq₁/(4π∈₀μg²), Aℓ(p) is as defined in problem 20.5, and A = λ_D/b₀. For ⋀ ≫ 1 verify that

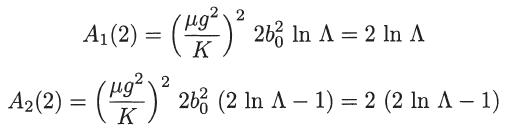
Note that, since K = qq₁/(4π∈₀) for the coulomb interaction potential, we have (μg²/K)² b₀² = 1.

Data from Problem 20.5.

From the expression for σ_m, obtained in part (a) of problem 20.4, verify that for p = 2 the momentum transfer cross section is given by

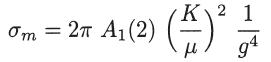
where A₁(2) is given by (with ℓ = 1 and p = 2)

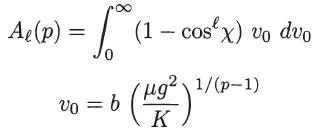
Consequently, the velocity-dependent collision frequency, defined by

varies as g^–3 . This inverse dependence on g accounts for the so-called electron runaway effect. This implies that in the presence of a sufficiently large electric field E, some electrons will gain enough kinetic energy between collisions so as to decrease their cross section and the collision frequency, which in turn allows them to pick up more energy from the field and decrease even further their cross section and collision frequency. If E is large enough, the collision frequency may fall so fast that these electrons will form an accelerated beam of runaway electrons.

Transcribed Image Text:

Hg2 2 K A2 (2) = = A1 (2) (1) 2 263 [ in (1 + 12) – k b In (1 + 12) 12 (1 + A²)]