Consider an electron gas immersed in a uniform magnetostatic field B₀ and characterized by the following modified Maxwellian distribution function:

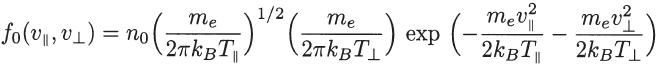
Use this distribution function in the dispersion relation for the right circularly polarized transverse wave propagating along B₀, given in (2.69), and evaluate the integrals to obtain the following dispersion relation

where

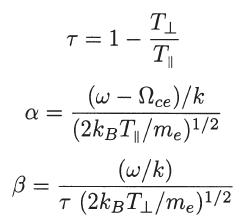
Analyze this dispersion relation to verify the existence or not of instabilities (positive imaginary part of ω) and/or damping (negative imaginary part of ω) of the wave amplitude, considering the propagation coefficient k = kẑ to be real. Determine the cyclotron damping coefficient. Analyze also the results considering the isotropic case for which T_∥ = T_⊥.

Equation 2.69.

Transcribed Image Text:

me 1/2 fo(v₁, ₁) = no (2 KT₁) ¹² (2 KT) exp mev 2kBT₁ - mev² 2kBT₁