Consider the motion of an electron in a spatially uniform magnetic field B = B_zẑ, such that B_z has a slow time variation given by

where B₀ and α are positive constants, and |αt| ≪ 1. Assume the following
initial conditions: r(0) = (r_c, 0, 0) and v(0) = (0, v_⊥0, 0), where r_c is the Larmor radius, V_⊥0 = Ω_cr_c and Ω_c = |q| B₀/m.

(a) Write the equation of motion, considering the Lorentz force, and solve it by a perturbation technique including only terms up to the first order in the small parameter a. Show that the particle velocity is given by

(b) Show that the particle orbit is given by

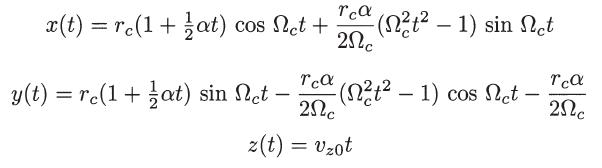
(c) Determine the orbital magnetic moment and verify its adiabatic invariance, retaining only terms up to the first order in α.

Transcribed Image Text:

B₂ (t) = Bo(1 - at)