Consider the motion of a charged particle in a spatially uniform magnetic field that varies slowly in
Question:
Consider the motion of a charged particle in a spatially uniform magnetic field that varies slowly in time as compared to the particle cyclotron period.
(a) Show that the equation of motion can be written in vector form as
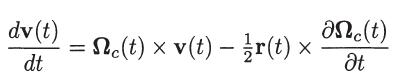
where Ωc(t) = –qB(t)/m.
(b) Considering that B(t) = ẑB0f(t), where B0 is constant, obtain the following equations for the motion of the particle in the plane normal to B:
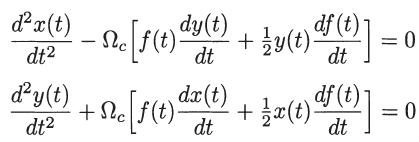
where Ωc = |q| B/m.
(c) Define a complex variable u(t) = x(t) + iy(t) and a function ξ(t) by
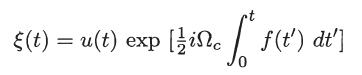
and show that the equation satisfied by ξ(t) is
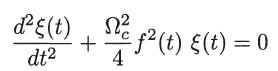
(d) If ξ1(t) and ξ2(t) are two linearly independent solutions of this equation, subject to the initial conditions
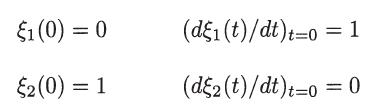
show that the solution for u(t) can be written as
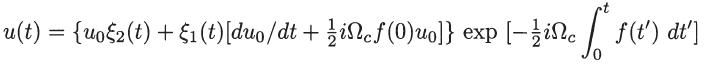
where u0 and du0/dt represent the initial position and velocity, respectively.
(e) Considering now that the particle is initially (t = 0) at the origin and moving with velocity v0 along the negative y axis, that is, u0 = 0 and du0/dt = –iv0, show that
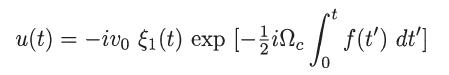
and, consequently,
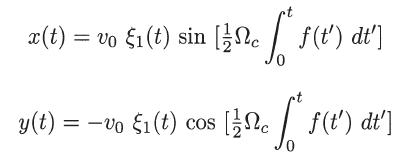
Step by Step Answer:






