(a) Assume that f(t), in problem 4.9, is given by exp (t). Show that, in this case,...

(a) Assume that f(t), in problem 4.9, is given by exp (–αt). Show that, in this case, ξ(t) satisfies the Bessel equation of zero order,

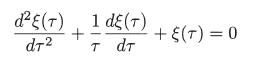
where τ = (Ω_c/2α) exp (–αt). Determine the two solutions of this equation which satisfy the initial conditions stated in problem 4.9 and interpret them physically.

(b) Considering now that f(t) = ( 1 – αt), solve the equation for ξ(t) in problem 4.9 in a power series in α, and determine the particle trajectory to order α. Show that the ratio ( v_x² + v_y²)/B(t) has no terms of order a, thus verifying the adiabatic in variance of the magnetic moment. Compare these results with those of problem 4.8.

Data from Problem 4.8.

Consider the motion of an electron in a spatially uniform magnetic field B = B_zẑ, such that B_z has a slow time variation given by

where B₀ and α are positive constants, and |αt| ≪ 1. Assume the following
initial conditions: r(0) = (r_c, 0, 0) and v(0) = (0, V_⊥0, 0), where r_c is the Larmor radius, V_⊥0 = Ω_cr_c and Ω_c = |q| B₀/m.

Data from Problem 4.9.

Consider the motion of a charged particle in a spatially uniform magnetic field that varies slowly in time as compared to the particle cyclotron period.

Show that the equation of motion can be written in vector form as

where Ω_c(t) = –qB(t)/m.

Considering that B(t) = ẑB₀f(t), where B₀ is constant, obtain the following equations for the motion of the particle in the plane normal to B:

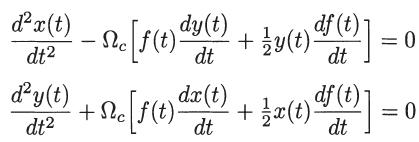
where Ω_c = |q| B/m.
Define a complex variable u(t) = x(t) + iy(t) and a function ξ(t) by

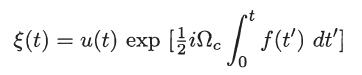
and show that the equation satisfied by ξ(t) is

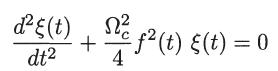
If ξ₁(t) and ξ₂(t) are two linearly independent solutions of this equation, subject to the initial conditions

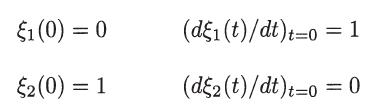
show that the solution for u(t) can be written as

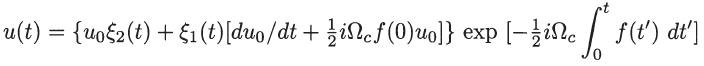
where u₀ and du₀/dt represent the initial position and velocity, respectively.

Considering now that the particle is initially (t = 0) at the origin and moving with velocity v₀ along the negative y axis, that is, u₀ = 0 and du₀/dt = –iv₀, show that

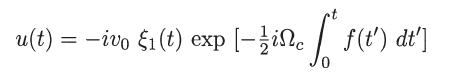
and, consequently,

Transcribed Image Text:

ď² (T) d7² 1 de (T) + T dr + ε(T) = 0