Question: 131 Time to solve a math programming problem. IEEE Transactions presented a hybrid algorithm for solving a polynomial zeroone mathematical programming problem. The algorithm incorporates

131 Time to solve a math programming problem. IEEE Transactions presented a hybrid algorithm for solving a polynomial zero–one mathematical programming problem.

The algorithm incorporates a mixture of pseudo-

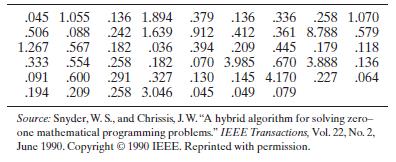
Boolean concepts and time-proven implicit enumeration procedures. Fifty-two random problems were solved by the hybrid algorithm; the times to solution (CPU time in seconds) are listed in the accompanying table and saved in the MATHCPU file.

a. Estimate, with 95% confidence, the mean solution time for the hybrid algorithm. Interpret the result.

b. How many problems must be solved to estimate the mean m to within .25 second with 95% confidence?

*c. Form a 95% confidence interval for the true standard deviation of the solution times for the hybrid algorithm.

Interpret the result.

.045 1.055 136 1.894 .506 .088 .242 1.639 379 .136 336 .258

.045 1.055 136 1.894 .506 .088 .242 1.639 379 .136 336 .258 1.070 912 .412 .361 8.788 .579 .394 209 .445 .179 .118 1.267 567 .182 .036 .333 .554 .258 .182 .070 3.985 .670 3.888 .136 .091 .600 .291 .327 .291 .327 130 145 4.170 .227 .064 .194 209 .258 3.046 .045 .049 .079 Source: Snyder, W. S., and Chrissis, J. W. "A hybrid algorithm for solving zero- one mathematical programming problems." IEEE Transactions, Vol. 22, No. 2, June 1990. Copyright 1990 IEEE. Reprinted with permission.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Fundamentals Of Statistics Questions!

Let r and s be solutions to the quadratic equation x 2 b x + c = 0. For n N, define d0 = 0 d1 = r s dn = b dn1 c dn2 (n 2) Prove that dn = r n s n for all n N. [4 marks] (b) Recall that a commutative...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Give Correct ANSWERS Human-Computer Interaction (a) If you had been one of the original inventors of the WIMP interface, and engineers on the technical team had been sceptical about the advantages...

can you please Summerize each section Use of Artificial Intelligence in Software Development Life Cycle: A state of the Art Review Bhagyashree W. Sorte, Pooja P. Joshi, Prof, Vandana Jagtap...

Please help me make an Executive Summary. Explain what you will examine in the case study. Write an overview of the field you are researching. Make a thesis statement and sum up the results of your...

POPULATION MODELS Problem 1. Yeast population growth You looked at how populations grow on problem 10 of Homework 4. Here, we will revisit population growth by examining how a population of yeast...

ONLY SOLVE FOR 13-2. I DO NOT NEED 13-1. PLEASE ONLY SOLVE 13-2 based on 13-1 information. PLEASE SOLVE ASAP Chapter 13 Translation of Financial Statements of Foreign Affiliates The account balances...

Hello again. This paragraph is same with previous I.L.A.C solving paragraph. But different question in there. It is for more for 'Remedy' so you can take less time to solve it because you know the...

1. A random sample of n = 4 scores is obtained from a population with a mean of = 80 and a standard deviation of = 10. If the sample mean is M = 90, what is the z -score for the sample mean? z =...

Calculus Writing Assignment: Modeling Using Differential Equations Each portion of each problem is worth 5 points. Total Points: 75 Answer each of the problems. Make sure to show all your work....

)Fred and Ida have discovered that if they get divorced in December of this year, file as single taxpayers, and then remarry in the following year, the arrangement would result in significant tax...

1. Which type of product is Sunny D? 2. When Sunny D enters into Oman market, which brands would be competitors of Sunny D? 3. Create a value proposition for Sunny D. Sunny D was once a highly...

2. Work study uses techniques like ________ and ______ _

What is the fraction of acid ionized in each acid in Exercise 15.64? Exercise 15.64 Use the K a values in Table 15.6 to calculate the pH of the following solutions. (a) 0.050 M HI (b)0.85 M HF...

Let X be a random variable with the following probability distribution: Find s(x) where g (X) = (2X +1)2, -3 6 1/6 1/2 1/3 1/3 7(2) g(X) = (2x + 1)?. %3D

Find the expected value of the random variable g(X) = X2, where X has the probability distribution of Exercise 4.2.

A large industrial firm purchases several new word processors at the end of each year, the exact number depending on the frequency of repairs in the previous year. Suppose that the number of word...

Future Value Computation What amount will be accumulated in four years if $10,000 is invested every six months beginning is six months and ending four years from today? Interest will accumulate at an...

6 (10 marks) Acme Co is looking to acquire Value Co at the end of the current year. Acme generates free cash flows of $2,500,000 in next year, which will increase by 5% in perpetuity. Acme's weighted...

Which of the following is NOT true regarding emerging growth companies? OA. They must submit a confidential draft registration statement with the SEC OB. They must not have issued more than $1...