179 Sale prices of apartments. A Minneapolis, Minnesota, real-estate appraiser used regression analysis to explore the relationship between the sale prices of apartment buildings sold in Minneapolis and various characteristics of the properties. Twenty-five apartment buildings were randomly sampled from all apartment buildings that were sold during a recent year. The table on the next page

(saved in the MNSALES file) lists the data collected by the appraiser. [ Note : The physical condition of each apartment building is coded E (excellent), G (good), or F (fair).]

a. Write a model that describes the relationship between sale price and number of apartment units as three parallel lines, one for each level of physical condition.

Be sure to specify the dummy-variable coding scheme you use.

b. Plot y against x1 (number of apartment units) for all buildings in excellent condition. On the same graph, plot y against x1 for all buildings in good condition.

Do this again for all buildings in fair condition. Does it appear that the model you specified in part a is appropriate? Explain.

c. Fit the model from part a to the data. Report the least squares prediction equation for each of the three building condition levels.

d. Plot the three prediction equations of part c on a scatterplot of the data.

e. Do the data provide sufficient evidence to conclude that the relationship between sale price and number of units varies with the physical condition of the apartments?

Test, using a = .05.

f. Check the data set for multicollinearity. How does your result affect your choice of independent variables to use in a model for sale price?

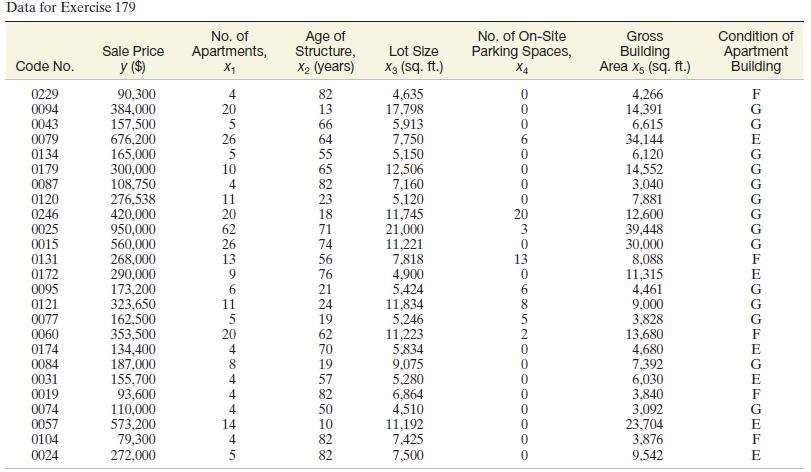
g. Consider the first-order model E(y) = b0 + b1 x1 + g+ b5 x5. Conduct a complete residual analysis for the model to check the assumptions on e.

Transcribed Image Text:

Data for Exercise 179 Sale Price No. of Apartments, Age of Structure, Code No. y ($) X2 (years) Lot Size X3 (sq. ft.) No. of On-Site Parking Spaces, X4 Gross Building Area X5 (sq. ft.) Condition of Apartment Building 0229 90,300 4 0094 384,000 20 0043 157,500 0079 676,200 26 0134 165,000 5 0179 300,000 10 0087 108,750 4 0120 276,538 11 0246 420,000 20 0025 950,000 62 0015 560,000 26 0131 268,000 13 0172 290,000 9 0095 173,200 6 0121 323,650 11 0077 162,500 5 0060 353,500 20 0174 134,400 4 0084 187,000 8 0031 155,700 4 0019 93,600 4 0074 110,000 0057 573,200 14 0104 79,300 0024 272,000 4445 4 10 5 BANNERUNK 82 4,635 13 17,798 66 5,913 64 7,750 55 5,150 65 12,506 82 7,160 23 18 5,120 11,745 71 21,000 74 11,221 56 7,818 13 76 4,900 21 5,424 24 11,834 19 5,246 62 11,223 70 5,834 19 9,075 57 5,280 82 6,864 50 4,510 11,192 82 7,425 82 7,500 00060000 g 30 30 6520000ooooo 4,266 14,391 6,615 34,144 6,120 14,552 3,040 7,881 12,600 39,448 30,000 8,088 11,315 4,461 9,000 3,828 13,680 4,680 7,392 6,030 3,840 3,092 23,704 3,876 9,542 ECCECGGGGGGFEGGGFEGEFCEFD