Consider a risky asset price \(\left(S_{t}ight)_{t \in \mathbb{R}}\) modeled in the Cox et al. (1985) (CIR) model as
\[
\begin{equation*}
d S_{t}=\beta\left(\alpha-S_{t}ight) d t+\sigma \sqrt{S_{t}} d B_{t}, \quad \alpha, \beta, \sigma>0 \tag{6.35}
\end{equation*}
\]
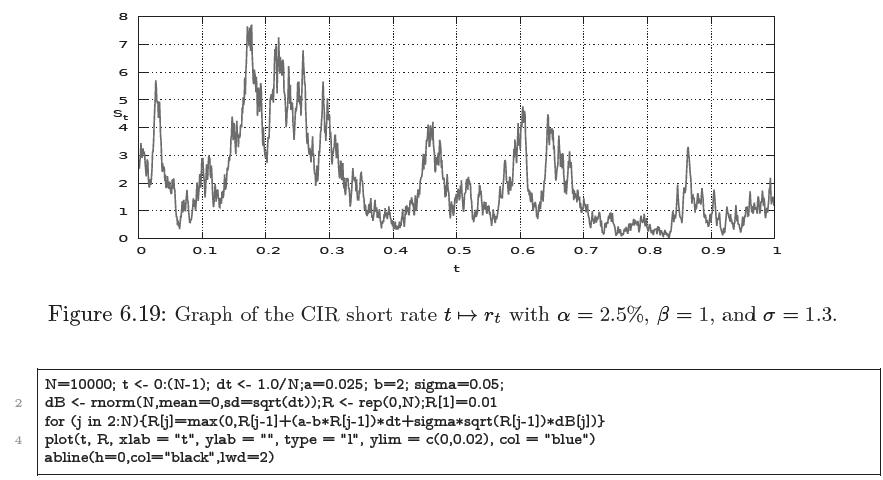
and let \(\left(\eta_{t}, \xi_{t}ight)_{t \in \mathbb{R}_{+}}\)be a portfolio strategy whose value \(V_{t}:=\eta_{t} A_{t}+\xi_{t} S_{t}\), takes the form \(V_{t}=g\left(t, S_{t}ight), t \geqslant 0\). Figure 6.19 presents a random simulation of the solution to (6.35) with \(\alpha=0.025, \beta=1\), and \(\sigma=1.3\).

Based on the self-financing condition written as \[
\begin{align*}
d V_{t} & =r V_{t} d t-r \xi_{t} S_{t} d t+\xi_{t} d S_{t} \\
& =r V_{t} d t-r \xi_{t} S_{t} d t+\beta\left(\alpha-S_{t}ight) \xi_{t} d t+\sigma \xi_{t} \sqrt{S_{t}} d B_{t}, \quad t \geqslant 0 \tag{6.36}
\end{align*}
\]
derive the PDE satisfied by the function \(g(t, x)\) using the Itô formula.

Transcribed Image Text:

2 4 8 7 6 St 4 3 2 1 O 0.1 0.2 0.3 0.4 0.5 t 0.6 0.7 0.8 N=10000; t